J A S O N B E H R S T O C K
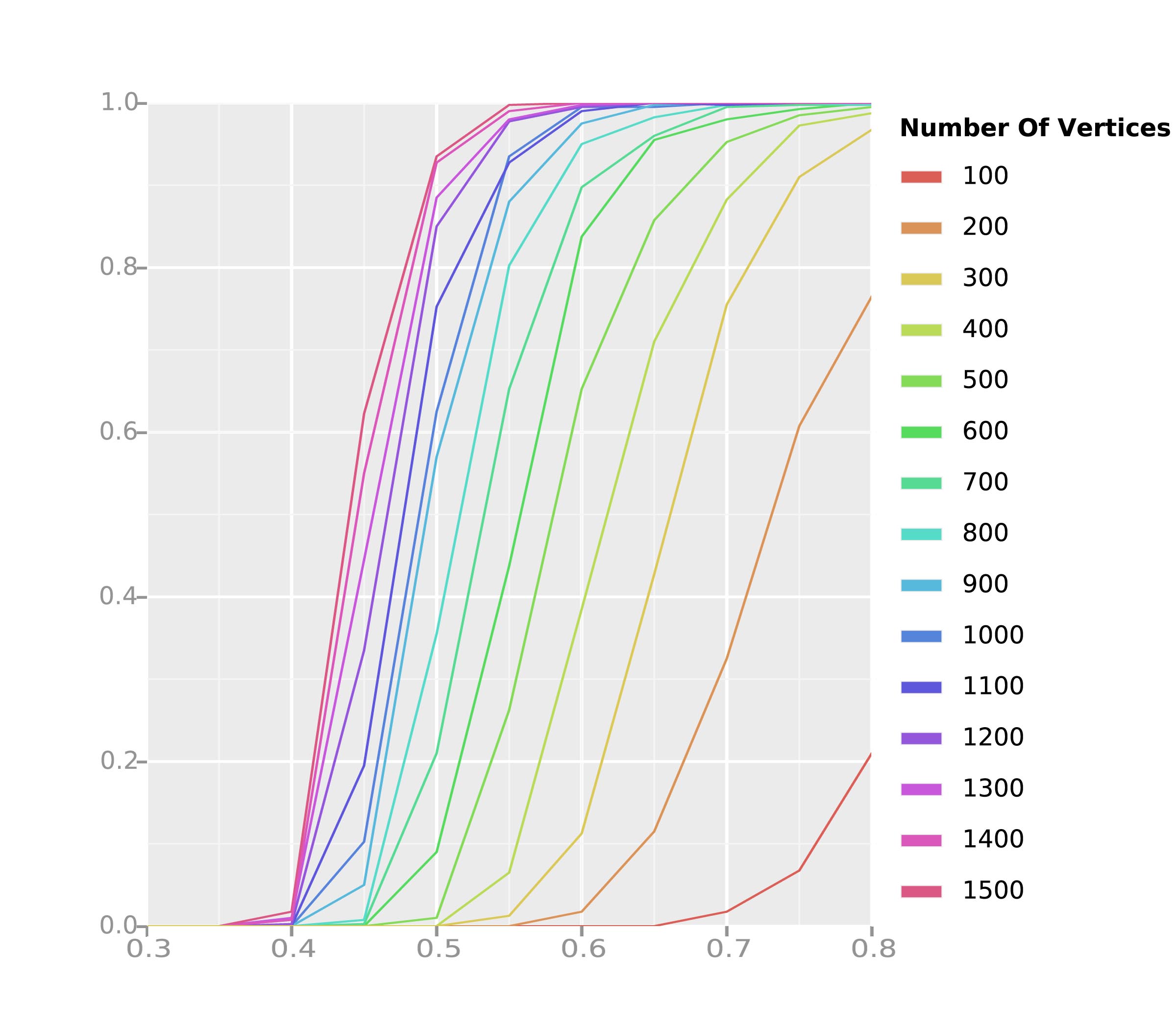
The following applet, written by Christopher Manning, allows you to visualize random graph as you vary the vertex count and density:
Some papers I've recently written which involve random graphs are:
-
Connectivity for square percolation and coarse cubical rigidity
in random right-angled Coxeter groups, with
A. Ciceksiz and
V. Falgas-Ravry
Supplementary source code for computing square graphs and also the data set for the examples constructed in the paper. -
A threshold for relative hyperbolicity in random right-angled Coxeter groups, with
A. Ciceksiz and
V. Falgas-Ravry
Advances in Mathematics, vol 482, 2025.
-
Square percolation and the threshold for quadratic divergence in random right-angled Coxeter groups, with
V. Falgas-Ravry and T.
Susse
Random Structures and Algorithms, vol. 60, 594-640, 2022. -
Global structural properties of random graphs, with
V. Falgas-Ravry,
M.
Hagen and T.
Susse
International Mathematics Research Notices, vol. 2018, 1411-1441, 2018.
-
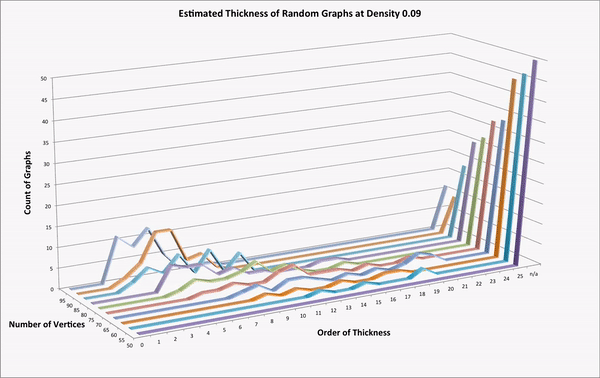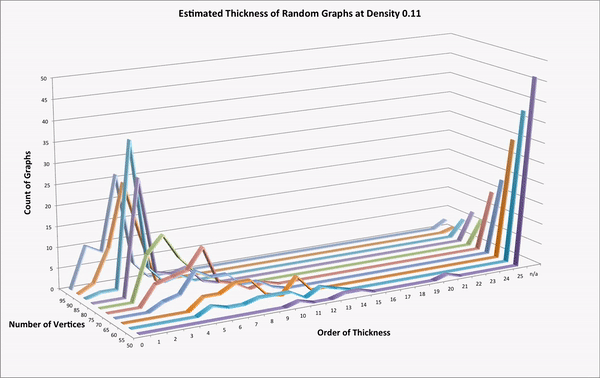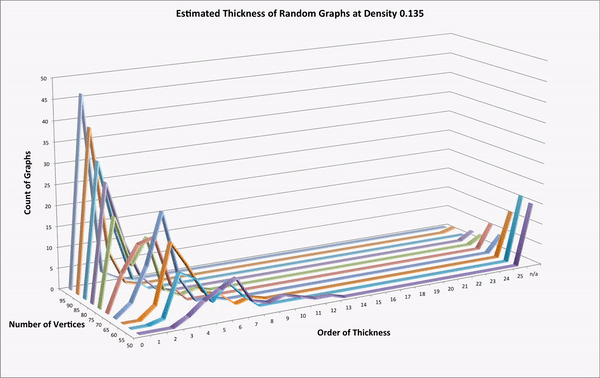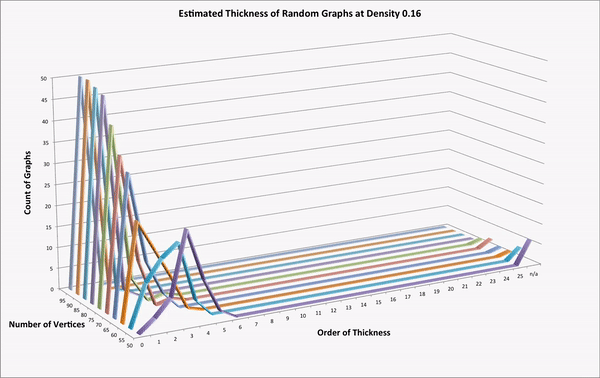
Thickness, relative hyperbolicity, and randomness in Coxeter
groups, with
M.
Hagen and A.
Sisto, with an appendix written jointly with P.-E.
Caprace
Algebraic & Geometric Topology, vol. 17, 705-740, 2017.
- AS checks for being an "augmented suspension".
- CFS checks for having the "constructed from squares" property.
- LGT checks whether or not a graph yields a relatively hyperbolic right-angled coxeter group.
- TEA, was written by Robbie Lyman, and computes upper bounds on the order of thickness of the right-angled Coxeter group associated to a graph. Details about his program are available in his undergraduate thesis, which I supervised, Algorithm computations of thickness in right-angled Coxeter groups
Please send any feedback or questions about the software to me at: jason.behrstock@lehman.cuny.edu